解答例:練習問題_5_1 20個のボール
問題文との対応が取りやすいので、集合の演算は演算子を使用しました。
# sからiの倍数の部分集合を取り出す関数
def fa(i, s):
return {x for x in s if x%i ==0 }
omg = set(range(1, 21))
a2, a3, a5 = fa(2, omg), fa(3, omg), fa(5, omg)
print('1.', '\n', 'omg: ', omg, '\n',
'a2: ', a2, '\n',
'a3: ', a3, '\n',
'a5: ', a5, '\n', '\n',
'2.', '\n',
'a2 ∩ (a3 ∪ a5): ', a2 & (a3 | a5), '\n',
'(a2 ∩ a3) ∪ (a2 ∩ a5): ', (a2 & a3) | (a2 & a5), '\n',
'a2 ∩ (a3 ∪ a5) == (a2 ∩ a3) ∪ (a2 ∩ a5): ',
a2 & (a3 | a5) == (a2 & a3) | (a2 & a5), '\n', '\n',
'3.', '\n',
'a2 ∪ (a3 ∩ a5): ', a2 | (a3 & a5), '\n',
'(a2 ∪ a3) ∩ (a2 ∪ a5): ', (a2 | a3) & (a2| a5), '\n',
'a2 ∪ (a3 ∩ a5) == (a2 ∪ a3) ∩ (a2 ∪ a5): ',
a2 | (a3 & a5) == (a2 | a3) & (a2 | a5), '\n', '\n',
'4.', '\n',
'(a2 ∪ a3)c: ', omg - (a2 | a3), '\n',
'a2c ∩ a3c: ', (omg - a2) & (omg - a3), '\n',
'(a2 ∪ a3)c == a2c ∩ a3c: ',
omg - (a2 | a3) == (omg - a2) & (omg - a3), '\n', '\n',
'5.', '\n',
'(a2 ∩ a3)c: ', omg - (a2 & a3), '\n',
'a2c ∪ a3c: ', (omg - a2) | (omg - a3), '\n',
'(a2 ∩ a3)c == a2c ∪ a3c: ',
omg - (a2 & a3) == (omg - a2) | (omg - a3), '\n', '\n',
'6.', '\n',
'a2 △ a3: ', a2 ^ a3, '\n',
'a2c △ a3c: ', (omg - a2) ^ (omg - a3), '\n',
'(a2 ∪ a3) \\ (a2 ∩ a3): ', (a2 | a3) - (a2 & a3), '\n',
'a2 △ a3 == a2c △ a3c == (a2 ∪ a3) \\ (a2 ∩ a3): ',
a2 ^ a3 == (omg - a2) ^ (omg - a3) == (a2 | a3) - (a2 & a3), '\n', '\n',
'7.', '\n',
'P(a2 ∪ a3): ', len(a2 | a3)/len(omg), '\n',
'P(a2) + P(a3) - P(a2 ∩ a3): ',
len(a2)/len(omg) + len(a3)/len(omg) - len(a2 & a3)/len(omg), '\n',
'P(a2 ∪ a3) == P(a2) + P(a3) - P(a2 ∩ a3): ',
len(a2 | a3)/len(omg) ==
len(a2)/len(omg) + len(a3)/len(omg) - len(a2 & a3)/len(omg),
sep='')1.
omg: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
a2: {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
a3: {3, 6, 9, 12, 15, 18}
a5: {10, 20, 5, 15}
2.
a2 ∩ (a3 ∪ a5): {6, 10, 12, 18, 20}
(a2 ∩ a3) ∪ (a2 ∩ a5): {18, 20, 6, 10, 12}
a2 ∩ (a3 ∪ a5) == (a2 ∩ a3) ∪ (a2 ∩ a5): True
3.
a2 ∪ (a3 ∩ a5): {2, 4, 6, 8, 10, 12, 14, 15, 16, 18, 20}
(a2 ∪ a3) ∩ (a2 ∪ a5): {2, 4, 6, 8, 10, 12, 14, 15, 16, 18, 20}
a2 ∪ (a3 ∩ a5) == (a2 ∪ a3) ∩ (a2 ∪ a5): True
4.
(a2 ∪ a3)c: {1, 5, 7, 11, 13, 17, 19}
a2c ∩ a3c: {1, 5, 7, 11, 13, 17, 19}
(a2 ∪ a3)c == a2c ∩ a3c: True
5.
(a2 ∩ a3)c: {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20}
a2c ∪ a3c: {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20}
(a2 ∩ a3)c == a2c ∪ a3c: True
6.
a2 △ a3: {2, 3, 4, 8, 9, 10, 14, 15, 16, 20}
a2c △ a3c: {2, 3, 4, 8, 9, 10, 14, 15, 16, 20}
(a2 ∪ a3) \ (a2 ∩ a3): {2, 3, 4, 8, 9, 10, 14, 15, 16, 20}
a2 △ a3 == a2c △ a3c == (a2 ∪ a3) \ (a2 ∩ a3): True
7.
P(a2 ∪ a3): 0.65
P(a2) + P(a3) – P(a2 ∩ a3): 0.65
P(a2 ∪ a3) == P(a2) + P(a3) – P(a2 ∩ a3): True
参考のため、各式に関するベン図を掲載します。
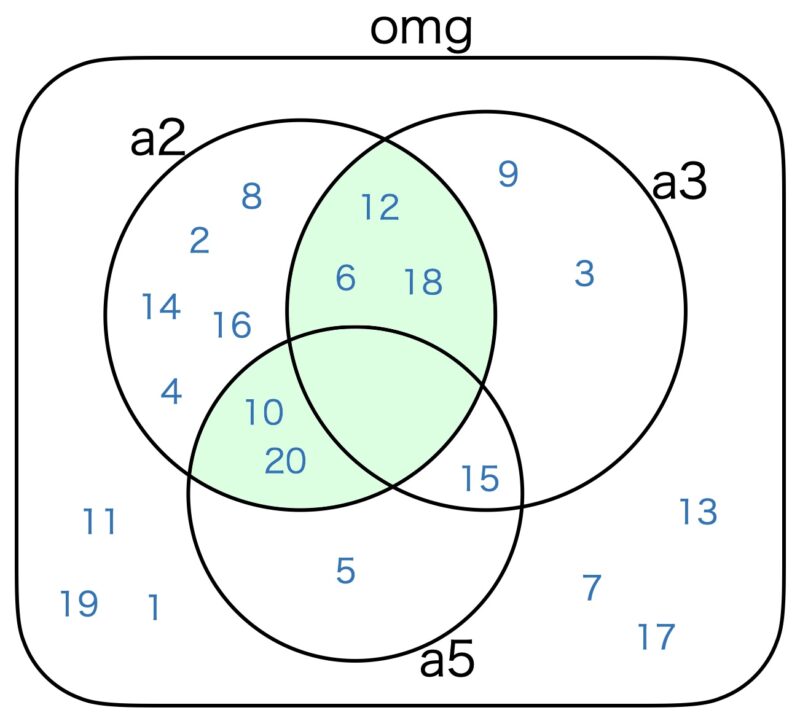
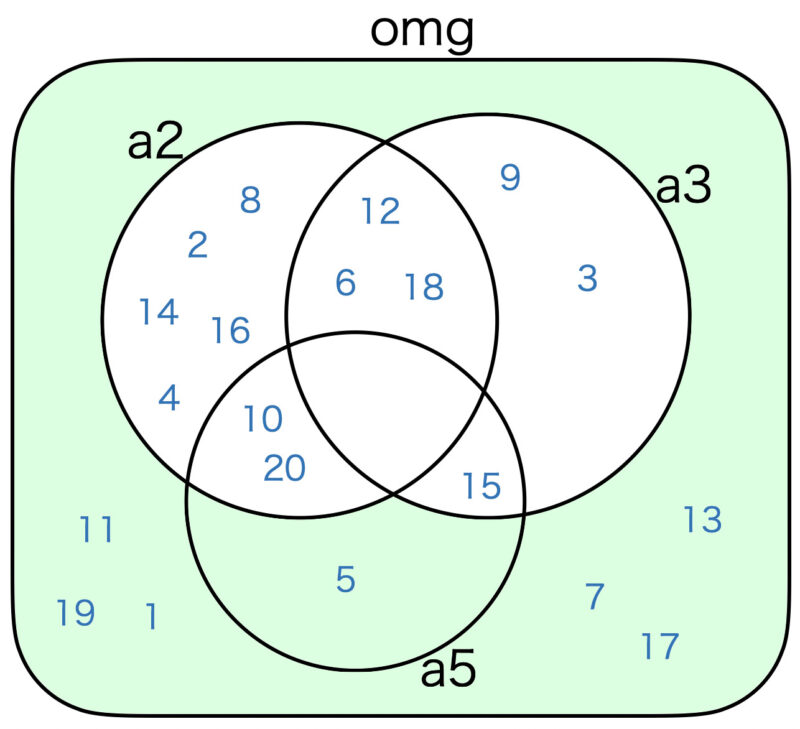
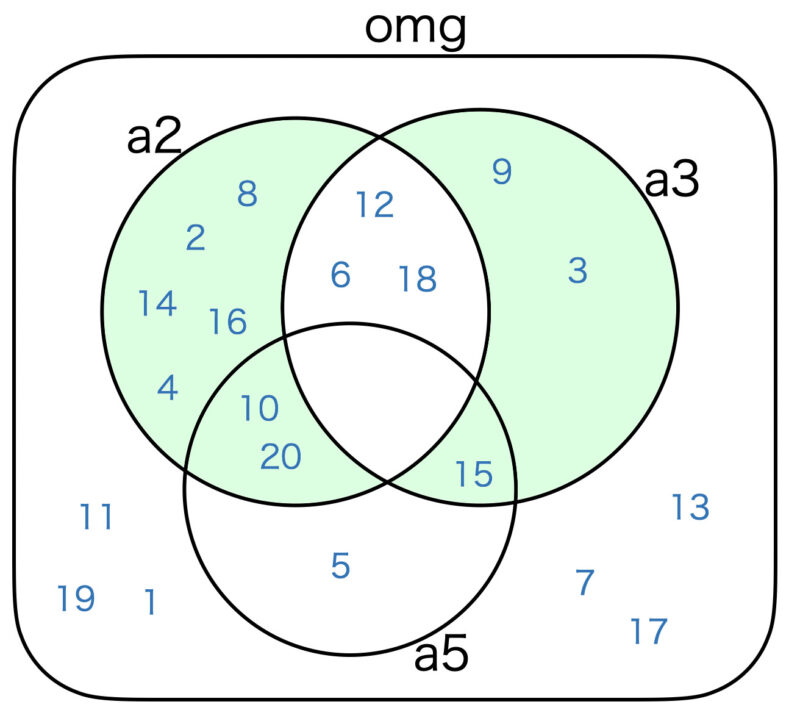
== (a2 ∪ a3) \ (a2 ∩ a3)
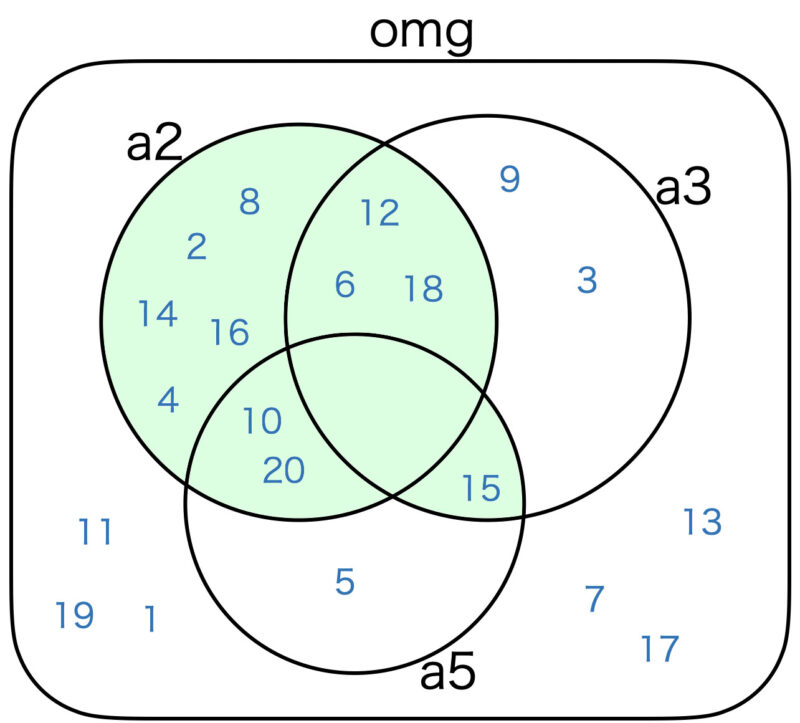
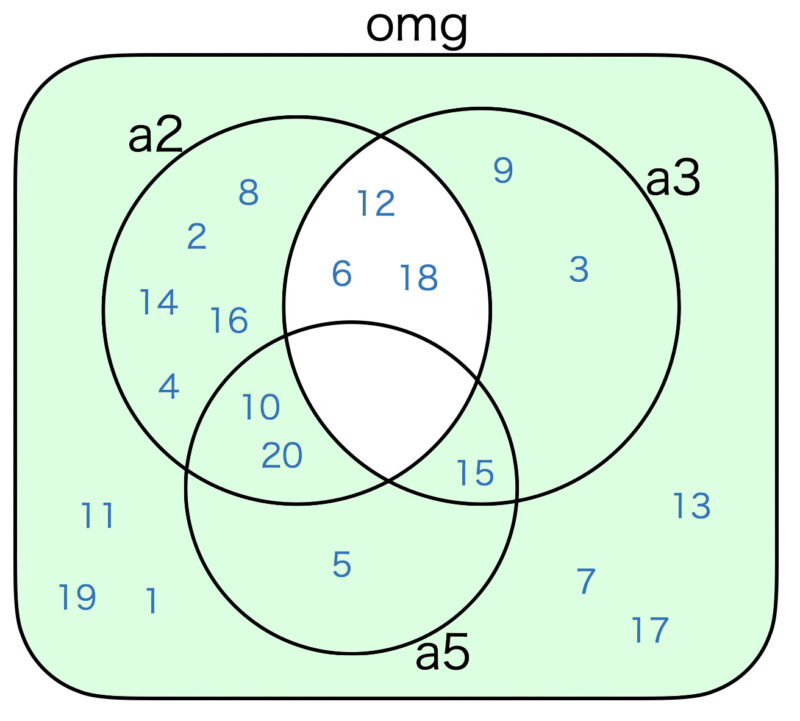
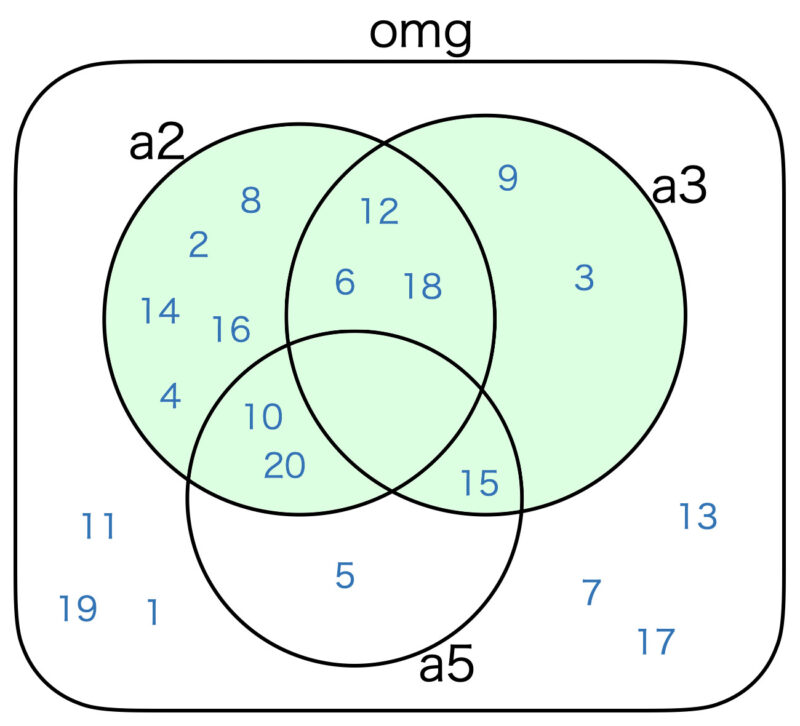
6番の様に print関数で \ を含む文字列を出力する場合は、エスケープシーケンスの \ をつけて、 \\ とする必要があります。

