- for文
- 例題_3_1 for ~ in リスト:
- 練習問題_3_1 for ~ in リスト:
- 例題_3_2 for ~ in リスト: からリストを作成
- 練習問題_3_2 for ~ in リスト: からリストを作成
- 例題_3_3 for ~ in range():
- 練習問題_3_3 for ~ in range():
- 例題_3_4 for ~ in range(len()):
- 練習問題_3_4 for ~ in range(len()):
- 補足 for i, x in enumerate(s):
- 練習問題_3_5 for文の関数化(フィボナッチ数列)
- 例題_3_5 forの2重化
- 練習問題_3_6(二次元のlist作成)
- 練習問題_3_7(forの2重化の応用)
- 練習問題_3_8(forの3重化 行列の積)
- 積の転置行列 公式の確認
- 練習問題_3_9(パスカルの三角形)
- 例題_3_6 int型を要素にもつlistの文字列化
- 練習問題_3_10(パスカルの三角形の出力)
- 例題_3_7 for if break else
- 練習問題_3_11(素数list)
- while文
- 実行時間の測定 time
- continue文 について
- iter, next と try, except
for文
はじめにループ処理で一番使われているfor文を紹介します。
for 変数 in シーケンス:
処理文for文の書き方は上記の様に、 for + 変数名 + in + シーケンス + コロン(:) を置きます。その下にインデントを入れて処理文(複数行可)を記載します。
シーケンス型の各要素に対してindexの順番に一つずつ取り出して繰り返し処理を行うのでforループとも呼ばれます。if文と共によく使用される制御文です。
例題_3_1 for ~ in リスト:
最初の例として、複数の植物(plants)の名前(str)のlistを定義して各要素の名前(文字数)を出力してみましょう。
plants = ['violet', 'rose', 'dandelion', 'pine tree', 'ginkgo']
for x in plants:
print(x+'('+str(len(x))+')')violet(6)
rose(4)
dandelion(9)
pine tree(9)
ginkgo(6)
上記for文で実際に内部で行われている処理は以下となります。
- はじめにシーケンス(plants)のindex 0の要素(‘violet’)を変数名(x)に格納し、処理(print)を実行して violet(6) を出力
- 次にindexに1を足して、それがまだシーケンス(plants)の長さ5より小さいかどうかを判定。
- 2がTrueの場合、そのindexの要素を変数名(x)に格納して処理(print)を実行。
- 3の後はまた2番に戻り、処理を繰り返す。2番の判定でindexがシーケンスの長さと同じになったところでforループ処理を終了。
for文では in の後のシーケンスは予め定義されている必要がありますが、inの前にある変数名(ここではx)はforループの中で要素を代入して使用するので、事前に定義されている必要はありません。
練習問題_3_1 for ~ in リスト:
漢字のリスト la = [‘春’, ‘日’, ‘空’, ‘気’, ‘土’, ‘雨’]
が与えられたとき、各要素の漢字とその後にコードポイントを出力してみましょう。
コードポイントとは文字毎に設定されている番号で、プログラム内ではすべて文字はこのコードポイントでやり取りされています。
コードポイントは ord() 関数で調べることができます。
例題_3_2 for ~ in リスト: からリストを作成
例題_3_1 で使用した複数の植物(plants)の名前(str)のリスト
plants = [‘violet’, ‘rose’, ‘dandelion’, ‘pine tree’, ‘ginkgo’]
が与えられたとき、各要素の文字数を要素とするリストを作成してみましょう。
plants = ['violet', 'rose', 'dandelion', 'pine tree', 'ginkgo']
counts = []
for x in plants:
counts.append(len(x))
counts[6, 4, 9, 9, 6]
上記コードでは、まず for文の前に counts に空のリストを代入します。
for 文の中で x で呼び出されるリスト plants の要素の文字数 len(x) を .append() メソッドを使ってcountsに追加していきます。
練習問題_3_2 for ~ in リスト: からリストを作成
漢字のリスト la = [‘春’, ‘日’, ‘空’, ‘気’, ‘土’, ‘雨’]
が与えられたとき、各要素のコードポイントのリストを作成してください。
例題_3_3 for ~ in range():
次は、1から50までの数字の中から5の倍数または7の倍数の数字を取り出してlistを作成するという問題です。以下の方針で作成します。
- 1から50までの数字を表すシーケンスには range(1, 51)を使用
- forの処理の中でif文を使用して5の倍数または7の倍数であるかどうかを判定
- 5の倍数または7の倍数の判定には (x%5 == 0) or (x%7 == 0) を使用
- 最初に空のlistを作成して、上記条件に一致する場合に appendメソッドで要素を追加
result = []
for i in range(1, 51):
if (i%5 == 0) or (i%7 == 0):
result.append(i)
result[5, 7, 10, 14, 15, 20, 21, 25, 28, 30, 35, 40, 42, 45, 49, 50]
この様に数字を順番に確認していく場合には range 関数を使用することが出来ます。注意点は range(50) とすると 0 ~ 49 の範囲となりますので、この問題の場合は range(1, 51) とする必要があります。
また、処理文にif文を使っていますので、if文の中の処理文(ここでは result.append(i))はインデントが2つ分(半角空白8個分)が必要となります。
練習問題_3_3 for ~ in range():
1 から 50 までの数字の中から 3 の倍数だが 2 の倍数ではない数字を取り出してlistを作成してください。
例題_3_4 for ~ in range(len()):
今度の例は、キーボードから文字列を入力すると使用している文字について、index(空白)文字(空白)Unicodeのコードポイント を全ての文字について出力するコードを作成します。例えば、キーボードから abc と入力すると
0 a 97
1 b 98
2 c 99
と出力されるコードです。以下の方針で作成します。
- キーボード入力をするためには x = input() を使用
- indexはrange(len())で発生させる
- 文字列から文字を取り出すときは 文字列[index] を使用
- Unicodeのコードポイントはord()関数を使用
s = input('-->')
for i in range(len(s)):
print(i, s[i], ord(s[i]))–> abc
0 a 97
1 b 98
2 c 99
- この様に input([prompt])関数を使用すると実行時にキーボードからstr(文字列)として入力することが出来ます。引数のprompt(ここでは’–>’)を入れて実行すると
 の様にpromptに続く形で入力ボックスが現れます。(promptを省略した場合はスペース1個)ここに例えば abc を入力してEnter(Return)を押すと上記の場合変数 s にstrの’abc’が代入され、同時に –> abc が出力されます。
の様にpromptに続く形で入力ボックスが現れます。(promptを省略した場合はスペース1個)ここに例えば abc を入力してEnter(Return)を押すと上記の場合変数 s にstrの’abc’が代入され、同時に –> abc が出力されます。 - range(len(sequence))を使用すれば、長さ不定のシーケンスのindexを生成することが出来ます。
- 文字列strはテキストシーケンス型に分類され、tupleと同じイミュータブル(immutable/文字の変更不可)シーケンスの一つです。従って[index]により文字を抽出することが出来ます。例. ‘abc'[1] -> ‘b’
上記コードでは日本語のような2バイト文字のコードポイントも確認できますので、いろいろ試してみてください。
練習問題_3_4 for ~ in range(len()):
キーボードから文字列を入力すると使用している文字について、index (空白) 文字 (空白) Unicodeのコードポイント(16進数) を全ての文字について出力するコードを作成してください。
10進数を16進数に変換するのは hex() 関数を使用します。
補足 for i, x in enumerate(s):
例題_3_4の様にinの後のシーケンスからindexと要素の両方を取り出したい時に組み込み関数のenumerate(iterable, start=0)を使用することも出来ます。
s = input('-->')
for i, x in enumerate(s):
print(i, x, ord(x))–> abc
0 a 97
1 b 98
2 c 99
forとinの間には、2つの変数(ここでは i と x)を置き、in の後にシーケンスを引数としたenumerate関数の戻り値であるenumerateオブジェクトを置きます。すると1番目の変数(i)には0から始まるindexが、2番目の変数(x)にはシーケンスの要素が格納されます。
以下はenumerate関数の引数である start = 1とした場合の結果です。( startのデフォルト値は0)
s = input('-->')
for i, x in enumerate(s, start = 1):
print(i, x, ord(x))–> abc
1 a 97
2 b 98
3 c 99
start = 1とすると、i には1から始まる番号が格納されます。
練習問題_3_5 for文の関数化(フィボナッチ数列)
フィボナッチ数列とは
0, 1, 1, 2, 3, 5, 8, 13, …
の様に、最初の数字が0、2番目の数字が1で3番目以降が i 番目の数字 = (i-2)番目の数字 + (i-1)番目の数字 で求められる数列です。つまり、
3番目の数字は 1番目の0 + 2番目の1 = 1
4番目の数字は 2番目の1 + 3番目の1 = 2
5番目の数字は 3番目の1 + 4番目の2 = 3
と続く数列です。
さて、ここでの問題は3以上の整数 n を引数として、nの長さのフィボナッチ数列を格納したlistを戻す関数 fibo(n) を作成して下さい。
なお、引数nが3以上の整数ではない場合、’引数には3以上の整数を使用してください’ とメッセージを出力してNoneを戻して下さい。
また、日本語でも良いのでdocstringを入れて下さい。
例題_3_5 forの2重化
for文の処理文の中にfor文を入れ子にすることが出来ます。
以下の様に十の位に行番号、一の位に列番号を表す数字を要素にもつ3×4の行列を表す二次元リストが与えられたとします。
以下はこの二次元のlistを定義してそれをフラット化(子listの要素を順番に全て取り出して一次元化)するコードです。
ls = [[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23]]
ls_flat = []
for row in ls:
for x in row:
ls_flat.append(x)
ls_flat[0, 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 23]
はじめにフラット化されるlistの ls_flat の初期値[]を設定します。
1段目の for row in ls: で row には始めに ls の子listである [ 0, 1, 2, 3] が入ります。
2段目の for x in row: で x には始めに row の要素が 0 から順番に入ります。
ls_flat.append(x) でそれらを順番に ls_flat の要素として格納していきます。
この様にfor文は二重三重〜と多重化が可能です。この機能を使って面倒な計算を一気に処理してしまうことが出来ますが、一方データ量が大きいときはその分コンピュータの処理時間もかかりますので注意が必要です。
練習問題_3_6(二次元のlist作成)
上記例題_3_5で使用している以下の ls を for文で作成する問題です。
ls = [[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23]]以下のような形で関数化して下さい。
- 関数名を create_2d_list(m, n) として下さい。mは行数、nは列数を表します。上記の例は m, n = 3, 4 です。
- i 行 j 列の位置の孫要素は 10*i + j で計算します。
- 引数m, n は共に自然数(1以上の整数)です。そうではない場合、’引数m, nには共に自然数を使用してください’ とメッセージを出力して、Noneを戻り値として下さい。
- 日本語で良いのでdocstringを入れて下さい。
練習問題_3_7(forの2重化の応用)
以下は例題_3_5で使用した二次元のlistです。
ls = [[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23]]これを入力データとして以下の様なlistを作成して下さい。このとき子listの長さは全て同じとします。
1番は関数化する必要はありませんが、2番は関数化して下さい。
- [0, 10, 20, 1, 11, 21, 2, 12, 22, 3, 13, 23] の様に縦に(column方向に)スキャンした形でflat化
- [[0, 10, 20], [1, 11, 21], [2, 12, 22], [3, 13, 23]] の様に行と列を入れ替えた二次元listを作成する関数 trans_2d_list(ls) を作成して下さい。これを行列の転置と言います。
尚この関数は練習問題_3_2で作成した関数のcreate_2d_list(3, 4)を引数とします。したがって最初のif文による引数確認、docstringは不要とします。
練習問題_3_8(forの3重化 行列の積)
さてここでは練習問題_3_2で作成したcreate_2d_list(m, n)で作成した2つの行例の積を計算する関数 mult_matrix(A, B) を作成します。以下の図は
A, B = create_2d_list(3, 4), create_2d_list(4, 4)
で作成した行列AとBの積であるABの計算方法を示したものです。
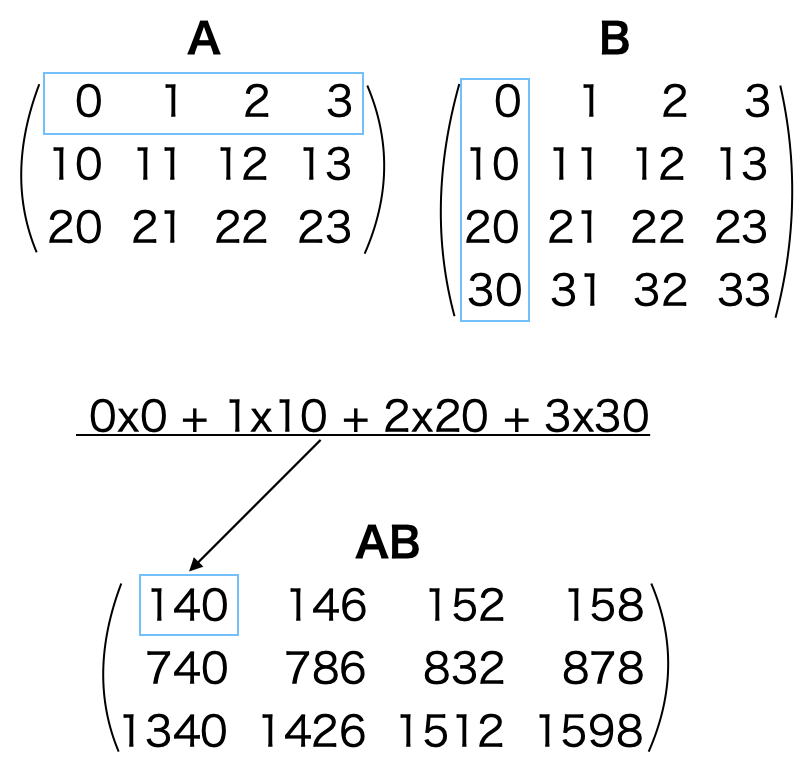
これからの説明は混乱を避けるためpythonの行列の数え方、すなわち最初の行を0行目、最初の列を0列目という言い方を用います。
積ABの0行0列目の要素は、Aの0行目とBの0列目のそれぞれの要素に対して初めから順番に掛け算した積の和を取ったものです。別の言い方ではAの0行目行ベクトルとBの0列目の烈ベクトルの内積とも言います。
積ABの i行 j列目の要素には、Aの i行目の行ベクトルとBの j列目の烈ベクトルの内積が入ります。従って、行列A(m行, k列) 行列B(k行, n列) の積ABは AB(m行, n列)となります。Aの列数(k)とBの行数(k)が同じ場合に掛け算が可能となります。
関数名はmult_matrix(A, B)、積の行列ABを戻り値とする関数を作成して下さい。AとBは練習問題_3_2で作成したcreate_2d_list(m, n)で作成しますので、引数の確認は不要とします。
日本語で良いのでdocstringを入れて下さい。
積の転置行列 公式の確認
さてここまで、行列の作成(create_2d_list(m, n))、転置(trans_2d_list(ls))、積(mult_matrix(A, B))の関数を作成しましたので、これらを使って行列の公式の一つである t(AB)=tBtA を確認してみようと思います。ちなみにtAは行列Aの転置行列を表します。
A, B = create_2d_list(3, 4), create_2d_list(4, 4)
tr, mu = trans_2d_list, mult_matrix
print('A:', A)
print('B:', B, '\n')
print('tr(mu(A, B)):', tr(mu(A, B)))
print('mu(tr(B), tr(A)):', mu(tr(B), tr(A)), '\n')
print('tr(mu(A, B)) == mu(tr(B), tr(A)):', tr(mu(A, B)) == mu(tr(B), tr(A)))A: [[0, 1, 2, 3], [10, 11, 12, 13], [20, 21, 22, 23]]
B: [[0, 1, 2, 3], [10, 11, 12, 13], [20, 21, 22, 23], [30, 31, 32, 33]]
tr(mu(A, B)): [[140, 740, 1340], [146, 786, 1426], [152, 832, 1512], [158, 878, 1598]]
mu(tr(B), tr(A)): [[140, 740, 1340], [146, 786, 1426], [152, 832, 1512], [158, 878, 1598]]
tr(mu(A, B)) == mu(tr(B), tr(A)): True
Aに3行4列、Bに4行4列の行列を代入します。
関数名が長いので、trに転置行列、muに行列の積の関数を代入します。
あとは、A、B、 t(AB)、tBtA の順に出力し、最後に t(AB)とtBtA について == を使って同じ(True)であることを確認しています。
ちなみにprint文にある’\n’ は追加の改行を意味しています。
練習問題_3_9(パスカルの三角形)
n列のパスカルの三角形をlistで戻す関数 pascals_triangle(n)を作成して下さい。
例えば pascals_triangle(7) を実行すると戻り値は
[[1],
[1, 1],
[1, 2, 1],
[1, 3, 3, 1],
[1, 4, 6, 4, 1],
[1, 5, 10, 10, 5, 1],
[1, 6, 15, 20, 15, 6, 1]]
となる様に作成します。パスカルの三角形の計算方法は以下の通り、
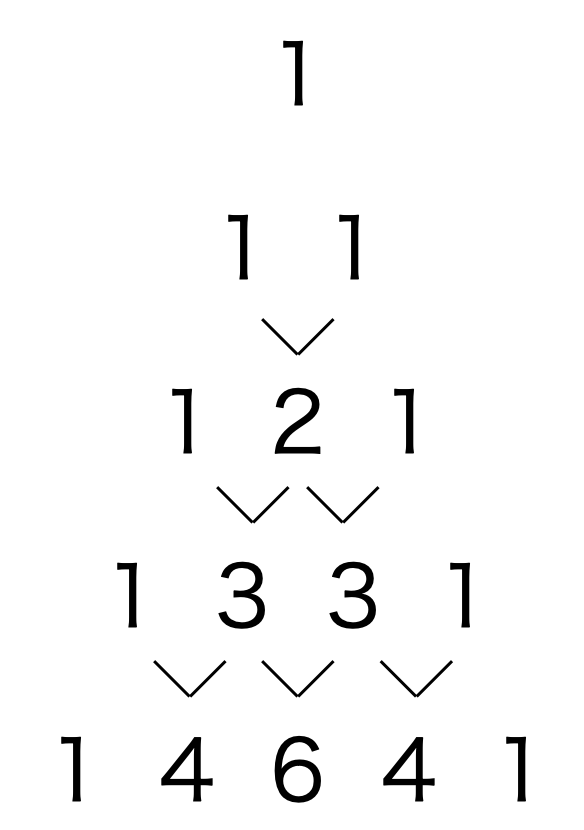
三行目の真ん中の2は、二行目のindex 0の1とindex 1の1の和
四行目のindex 1の3は、三行目のindex 0の1とindex 1の2の和
四行目のindex 2の3は、三行目のindex 1の2とindex 2の1の和
の様に続きます。
引数nは自然数(1以上の整数)ではない場合、’引数nには自然数を使用してください’ とメッセージを出力して下さい。
例題_3_6 int型を要素にもつlistの文字列化
ここで次の練習問題のためにint型を要素にもつlist [1, 3, 3, 1] から ‘1 3 3 1’という間にスペースを入れた一つの文字列を作成する例題を解いてみます。
ls = [1, 3, 3, 1]
st = ''
for x in ls:
st += str(x) + ' '
st = st[:-1]
st‘1 3 3 1’
- 作成するstr型の変数 st に空の文字列 ” を代入(listの時の [] に相当)
- for文で要素 x を取り出し str()関数でstr化したものを st に加え、さらにスペース ‘ ‘ を追加
- この状態では ‘1 3 3 1 ‘ となるので、st = st[:-1] で最後のスペースを削除
ここで、str(文字列)はimmutable(変更不可)なsequenceなので「最後のスペースを削除」出来ないのではと思われるかもしれません。tupleもそうですがimmutable(変更不可)なsequenceでも全体を再定義すれば変更ができます。st = st[:-1]は最後の文字を減らしたstrで再定義しているということになります。(stのidを調べて頂ければスペース削除前後で変わっていることが確認できます)
練習問題_3_10(パスカルの三角形の出力)
練習問題_3_9の戻り値であるパスカルの三角形のlistを以下のように三角形に出力する関数 print_pas(pas)を作成して下さい。
例えば print_pas(pascals_triangle(7)) を実行すると
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1の様な形に出力するものです。(等幅フォントでない場合は少し傾いた三角になることがあります)この関数は練習問題_3_9の関数pascals_triangleで作成したlistのみを引数としますので、引数が条件を満たすlistであるかどうかの確認は不要です。
ここではstr型のメソッドである str.center(width[, fillchar])を使用します。このメソッドはstrをwidthの文字数の真ん中になる様に両側にfillchar(指定しない場合は半角空白)を埋めてくれます。
例えば、x = ‘1 2 1’ の時 x.center(15) は ‘ 1 2 1 ‘と両側に5個の空白が入ってトータル文字数が15文字になります。
例題_3_7 for if break else
forループ処理の途中で、ある条件を満たした場合にforループを抜け出す時にはbreak 文を使用します。実際には forループの中で if文を使って条件を設定してその処理文として break 文を記載します。 但し、forループが全て修了しても if文の条件を満たすケースが無い時の処理を記載するために、elseが用意されています。
この例題として文字列(s)から特定の文字(c)が最初に現れるindex番号を戻し、文字(c)が文字列(s)に含まれていない場合は-1を戻す関数 get_index(s, c) を考えてみましょう。
def get_index(s, c):
for i, x in enumerate(s):
if x == c:
break
else: # sにcは含まれていない
i = -1
return i
get_index('Hello world!', 'l')2
- まず、enumerate関数を使用して文字列(s)からインデックス(i)と要素(x)をfor文で順番に取り出します。
- 取り出した要素(x)が引数のcに一致している場合はbreak文でforループから抜け出し、その時のindex(i)を戻します。この時は elseの処理は適用されません。
- 文字列の最後まで確認しても一致するものがない場合に else文が適用され i に -1 が代入されます。
この様にforループを途中で止める場合には break を使用します。forループ内で代入された変数 i, x は中断した時点での値が格納されており、同じ関数内であれば参照することが出来ます。
また elseは if のインデントの位置ではなく、forの位置にある事に注意して下さい。もし elseを ifの位置に置いた場合 x == c を満たさない全ての x に対して i = -1が適用されることになります。 forの位置にある事で、for文が完了した時点で breakの適用がなかった場合のみ、一度だけ i = -1が適用されます。
この例題では、elseの位置がどちらの場合でも(forの位置またはifの位置でも)結果は同じですが、次の練習問題の解答例の様にelseの処理にappendメソッドを使用する場合には、elseのインデントの位置を間違えると結果が異なってきます。このelseのインデントの位置を間違えない様にすることが重要です。
上記の例は ‘Hello world!’ という文字列で ‘l’ が最初に出るindex番号は 2 であることを示しています。
同じことをstrのfindメソッド(*)を使えば確認できます。
'Hello world!'.find('l')2
(*) strのメソッドである str.find(sub[, start[, end]])は文字列のスライス s[start:end] に部分文字列 sub が最初に現れるindexを戻します。一致するものが無い場合は -1 を戻します。
練習問題_3_11(素数list)
上記で学んだfor if break elseを使う練習問題です。
2以上の2つの整数 n_start, n_stop (n_start ≦ n_stop)を引数として、n_startからn_stopまでの全ての素数を小さい順に格納したlistを戻す関数 prime_num(n_start, n_stop) をfor if break elseを使用して作成して下さい。
素数の定義は「2 以上の自然数で、正の約数が 1 と自分自身のみであるもの」、もう少し分かり易く言いますと、2以上の整数で1と自分自身以外には割り切れない数です。
ある自然数 nが素数かどうかは、2から順番に割り切れるかどうかを確認していき、nの平方根以下まで確認すれば良いとされていますので、実行時間の節約のためにこの方法を使用したいと思います。
なお、引数が共に2以上の整数ではない場合、’引数にはn_start ≦ n_stopとなる2以上の整数を使用してください’ とメッセージを出力して、Noneを戻り値として下さい。
while文
for文よりも原始的なループ処理であるwhile文を紹介します。
while 条件:
処理文while文の書き方は上記の様に、whileの後に条件を記載してコロン(:)を置きます。その下にインデントを入れて処理文(複数行可)を記載します。条件がTrueの間、ずっと処理文を繰り返します。
whileのコードを書いていると時々無限ループに入ってしまうことがあります。その時jupyter labでは画面上部にある![]() の真ん中にある四角のボタン(Interrupt the Kernel)を押せば強制終了することができます。
の真ん中にある四角のボタン(Interrupt the Kernel)を押せば強制終了することができます。
以下は0.1秒の停止(スリープ)を繰り返すコードです。
import time
while True:
time.sleep(0.1)whileの条件がTrueなので、このコードは無限にスリープ状態を継続しています。ここを抜け出すにはInterrupt the Kernel ボタンで強制終了して下さい。
例題_3_8 while文でフィボナッチ数列
whileの例題として前節の練習問題で取り上げたフィボナッチ数列をwhile文で書いてみます。適当な正の整数(ここでは400)以下のフィボナッチ数列をlist化します。前節forの練習問題は長さnのlistでしたが、whileで書き易い様に問題設定を変えています。
# 400以下のフィボナッチ数列のlist
n, m = 0, 1
fibo = []
while n <= 400:
fibo.append(n)
n, m = m, n + m
fibo[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
- はじめにnとmの初期値をそれぞれ 0, 1と設定します。
- 次に作成listであるfiboを初期化 [] します。
- while文を記載し、条件を n <= 400 とします。
- 処理文で、fiboにnを追加し、nにmを、mにはn + mをそれぞれ代入します。
処理文を繰り返すうちに、nはフィボナッチ数列に従って大きくなります。while文の条件である n <= 400 がFalseになった時、すなわちnが400より大きくなった時点でwhile文は処理を止めます。
この様にwhile文の条件に含まれる変数処理文の中で再定義しながらループ処理を行うやり方が一般的です。
例題_3_9 while if break else
while文でもfor文と同様に while if break else の一連の組み合わせが使用できます。
例題_3_7 と同じ内容をwhile文で記載します。問題は、文字列(s)から特定の文字(c)が最初に現れるindex番号を戻し、文字(c)が文字列(s)に含まれていない場合は-1を戻す関数 get_index(s, c) です。
def get_index(s, c):
i = 0
while i < len(s):
if s[i] == c:
break
i += 1
else: # sにcは含まれていない
i = -1
return i
get_index('Hello world!', 'l')例題_3_7と見比べれば分かりますが、for -> whileで追加・変更したのは以下の点です。
- while文の前に i = 0 を定義
- whileの条件は i < len(s)
- if文の条件は s[i] == c
- if文の後で i に1を足す i += 1
breakは whileループを止めます。else は while が break しないで終了したときのみに適用されます。これらの点は for の場合と同じです。
練習問題_3_12(素因数分解 試し割り法)
まず、素因数分解について説明します。
素因数分解は自然数を素数の掛け算で表すことです。例えば 12546 という自然数が与えられた時
12546 = 2 x 32 x 17 x 41
の様に自然数12546をこれ以上割り切れない素数(2, 3, …)の掛け算として表すことを素因数分解と言います。
次に素因数分解の最も簡単な求め方である試し割り法について説明します。
与えられた自然数12546を試し割り法で素因数分解してみます。

- 12546を2から大きい方に順番に割り切れるかどうかを確認します。2で割り切れるのでその商 6273を下に記載します。(この時12546が素数かどうかの判定は練習問題_3_11と同様に平方根の小数点以下を切り捨てたint(12546**0.5)までの数字で割り切れないことを判定基準とします)
- 次に6273をまた2から大きい方に順番に割り切れるかどうかを確認します。3で割り切れるのでその商2091を下に記載します。
- 今度は2はすでに割り切れないことを確認済みなので、3から大きい方に順番に割り切れるかどうかを確認し、同様な処理を続けます。
- 最後に41の平方根は17よりも小さい数字ですので、割り算をするまでもなく素数であることが分かります。
この練習問題は、2以上の自然数 n を引数として、試し割り法で求めた n の素因数をlist化して戻す関数 trial_div(n) を作成して下さい。上記の例であれば、trial_div(12546)の戻り値は [2, 3, 3, 17, 41] となります。ループ処理はwhile, forのどちらを使用しても構いません。引数nが素因数を持たない素数の場合、[n] (nは具体的な数字、例えば[2], [1031] など)を戻します。
引数nが2以上の整数ではない場合、’引数には2以上の整数を使用してください’ とメッセージを出力して、Noneを戻り値として下さい。
実行時間の測定 time
条件分岐(if文)とループ処理(for文とwhile文) を覚えたところで、もう少し練習問題を解いてみましょう。
ここで time というモジュールを使って実行時間を測定してみたいと思います。プログラムの評価基準としてこれまで読み易いことに力点を置いてきましたが、ここからは実行時間が短いことも追加していきます。
実行時間を測定するためには import time で time というモジュールをimportする必要があります。試しに、練習問題_3_11の素数listを作成する関数 prime_num(2, 1000000)の実行時間を測定してみましょう。(以下のコードを実行前には必ずprime_num関数をdefで定義したコードを実行しておいて下さい)
import time
t_start = time.time()
answer = prime_num(2, 1000000)
print('run time: ', time.time() - t_start, '秒')
del answerrun time: 3.6198039054870605 秒
以上から100万までの素数をprime_numという関数で調べた際の実行時間は、筆者のPCでは約3.6秒かかったことになります。この時間はご使用のPCによって異なってきます。またPC上の他のプログラムの影響がありますので、実行時間には再現性はなく、再度実行しても必ずしも同じにはなりません。
上記コードはtimeという新しいモジュールをインポートして使用しています。
time はPCの時刻データを取り込むモジュールです。time.time() は timeというモジュールのtime()という関数で、UTC(1970/1/1を起点とする時刻)を秒単位で表しています。
t_start = time.time() で測定開始時間を t_start に格納し、測定終了時点で time.time() – t_start をprintすることで秒単位での実行時間を表示しています。
今回は実行時間の測定だけなので、del answer で 比較的大きなデータのanswerを削除しています。
練習問題_3_13(最大公約数① 単純な割り算)
最大公約数とは、2つ以上の正の整数に共通な約数(割り切れる数)の最大のものです。
ここから3問は全て2つの正の整数の最大公約数を3通りのやり方で解いてみて、アルゴリズムを変えれば実行時間が短くなることを感じてみましょう。
最初の方法は単純に1から順番に割り算をして割り切れる数の最大のものを最大公約数(g)として出力して、実行時間を測定しましょう。2つの自然数は以下です。
a, b = 46670393, 29699341
今回は関数化する必要はありません。ループ処理はfor, whileのどちらを使用しても構いません。また比較のために計算回数を数えるためのカウンターを入れて下さい。
練習問題_3_14(最大公約数② 素因数分解を参考に)
次は、練習問題 _3_12の素因数分解を参考にしてみます。
1から順番に公約数を確認していくのは上記①と同じですが、公約数が見つかった時にaとbを公約数で割り算して再度公約数を確認する方法です。この場合最大公約数は確認された全ての公約数の積となります。
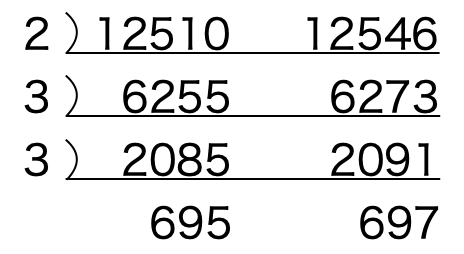
例えば上記例の場合、最大公約数は 2 x 3 x 3 = 18 となります
こちらの問題にも計算回数のカウンターを入れて下さい。
練習問題_3_15(最大公約数③ ユークリッド互除法)
最後に、最大公約数をユークリッド互除法を用いて解いてみます。
ユークリッド互除法が最大公約数に一致する数学的な証明については、申し訳ありませんがネット検索でご確認お願いします。
ユークリッドの互除法のウィキペディア(Wikipedia)の定義は以下の通りです。
2 つの自然数 a, b (a ≧ b) について、a の b による剰余を r とすると、 a と b との最大公約数は b と r との最大公約数に等しいという性質が成り立つ。この性質を利用して、 b を r で割った剰余、 除数 r をその剰余で割った剰余、と剰余を求める計算を逐次繰り返すと、剰余が 0 になった時の除数が a と b との最大公約数となる。
この問題は簡単なので、ヒントは無しでお願いします。while文でもfor文でもどちらでも結構です。
こちらにもカウンターを入れて下さい。
continue文 について
ここではcontinue文について簡単に説明します。
これまでループ処理を止めるbreak文と、何もしないpass文について説明しましたが、continueはその中間に位置し「continue以降の処理文をスキップしてループ処理を継続、シーケンスの次の要素に移る」という役割を果たします。continueについて余り深入りは避けたいと思います。と言うのはcontinue文を使わなくともコードは書けるからです。
breakと比較しながら continue について具体例で示します。
in_word = 'Hello World'
out_word = ''
for c in in_word:
if c == ' ':
break
out_word += c.upper()
out_word‘HELLO’
このコードは in_word を一文字ずつforループで読み込んでupperメソッドで大文字化しています。ただしスペース(‘ ‘)があった時には break されますので、そこで中断します。したがって out_wordは ‘HELLO’ となります。
この break を continue に変えてみましょう。
in_word = 'Hello World'
out_word = ''
for c in in_word:
if c == ' ':
continue
out_word += c.upper()
out_word‘HELLOWORLD’
out_wordは ‘HELLOWORLD’ です。これはスペース(‘ ‘)があった時には、その後の処理 out_word += c.upper() が省略されて次のループ処理に移行していることになります。
しかしわざわざcontinueを使わなくとも、もしスペースをカットしたいなら以下の様にすることも可能です。
in_word = 'Hello World'
out_word = ''
for c in in_word:
if c != ' ':
out_word += c.upper()
out_word‘HELLOWORLD’
この様に基本的にはcontinueがなければ書けないというコードは無い様に思われます。
おそらく continueは長い複雑なコードをデバッグしたり後から修正する際に、ループ処理の中である条件を満たすときにそれ以降のコードを既存の論理を変更せずにスキップしたいときに使用されます。
なので、continueについては、この便利な道具があることを頭の片隅にでも入れておけばよろしいかと思います。
iter, next と try, except
ここでは iter 関数と next 関数について、繰り返し処理の一種として一通り説明します。むしろついでに説明する try文 と except文 の方が重要かもしれません。
iter 関数は、引数が1つの場合と2つの場合があり、使い方が異なります。
引数が一つの iter 関数
引数が一つの場合 iter 関数はイテラブル iterable なオブジェクトを引数に取り、そのオブジェクトをイテレータ iterator として戻します。
イテラブル iterable なオブジェクトとは、要素を一度に 1 つずつ返せるオブジェクトです。これまで学んだオブジェクトのうち、シーケンス型(str, taple, range)や文字列(str)、そして今後紹介する集合型(set)や辞書型(dict)もイテラブルに含まれます。for文の in の後に使えるオブジェクトは全てイテラブルなオブジェクトとなります。
iter によって作成された イテレータ iterator のデータを一つずつ取り出す関数が、next です。next(iterator) を実行すると最初の要素が取り出され、再度 next(iterator) を実行すると次の要素が取り出されます。その様子を見てみましょう。
ls = [1, 2, 3]
print(ls, type(ls))
it = iter(ls)
print(it, type(it))
print(next(it)) # 1回目
print(next(it)) # 2回目
print(next(it)) # 3回目
print(next(it)) # 4回目[1, 2, 3] <class ‘list’>
<list_iterator object at 0x7fc3c0a00610> <class ‘list_iterator’>
1
2
3

上記 it はリスト ls = [1, 2, 3] に iter 関数を適用して作成した iterator です。print関数の中で next(it) を4回実行したところ、3回目までは要素が順番に出力されましたが、出し尽くした4回目にはエラーの様に「StopIteration」のメッセージが出て(これを例外 exceptionと言います)処理は中断されます。
この処理の中断を防ぐために試しに while 文を使って while it: としてみましょう。
ls = [1, 2, 3]
it = iter(ls)
while it:
print(next(it))1
2
3

while it: は it が True の間処理を繰り返しますが、全てのデータを出し尽くした後でも、iterator の it は Fail にはならないので、処理の中断を防ぐことはできません。
try 節 と except 節
例外による処理中断を防止する方法は、 try 節と except 節を以下の様にセットで使用することで可能となります。
ls = [1, 2, 3]
it = iter(ls)
while True:
try:
print(next(it))
except StopIteration:
break1
2
3
上記の様に try 節の後に except 節を置き、except の後に例外の名前を記載した場合の動作は以下の様になります。
- まず try 節の print(next(it)) が実行される
- そこで例外が発生しなければ except 節をスキップして try 文の実行を終わる
- 例外が発生し、それが設定した StopIteration であれば break が実行される
- 設定していない(StopIteration でない)例外が発生した場合は、処理が中断され例外処理が行われる。
例えば以下の様に、except で設定していない例外が現れた場合は、例外処理が実行されます。
ls = [-1, 0, 1, '2']
it = iter(ls)
while True:
try:
print(1 / next(it))
except StopIteration:
break-1.0
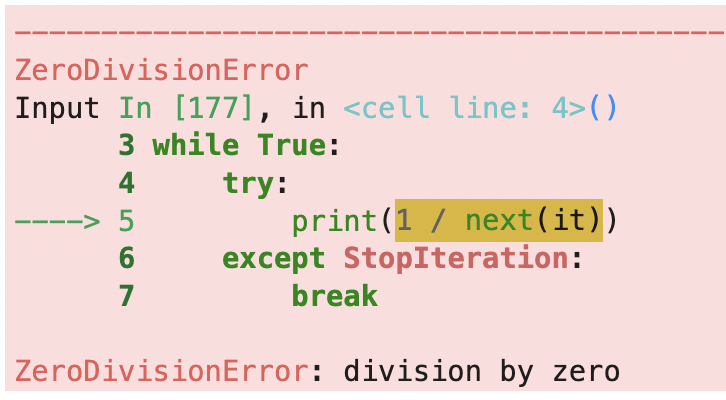
この様なの時には以下の様に、一つの try 節に対して 複数の except 節を置くことができますし、更には tuple にすることで一つの except 節で複数の例外を記載することも可能です。
ls = [-1, 0, 1, '2']
it = iter(ls)
while True:
try:
print(1/next(it))
except StopIteration:
break
except (ZeroDivisionError, TypeError):
print('invalid number')-1.0
invalid number
1.0
invalid number
except で設定していない時に処理を継続したい場合は、else 節を使用します。
ls = [-1, 0, 1, '2']
it = iter(ls)
ls2 = []
while True:
try:
x = 1/next(it)
except StopIteration:
break
except (ZeroDivisionError, TypeError):
pass
else:
ls2.append(x)
ls2[-1.0, 1.0]
ここで使用している pass 文は、処理を継続すると言う意味となります。
また、finally 節を使うと except 節の実行有無に関わらずどちらの場合の後でも処理を行うことができます。
ls = [-1, 0, 1, '2']
it = iter(ls)
ls2 = []
while True:
try:
y = next(it)
x = 1 / y
print(' ', end=' ')
except StopIteration:
print('end', end=' ')
break
except (ZeroDivisionError, TypeError):
print('err', end=' ')
else:
ls2.append(x)
finally:
print(y, '_Done', sep = '')
print('ls2:',ls2)-1_Done
err 0_Done
1_Done
err 2_Done
end 2_Done
ls2: [-1.0, 1.0]
引数が二つの iter 関数
引数が二つの場合、iter(callable, sentinel) で表され、第一引数は callable (呼び出し可能)なオブジェクトとなります。callable object とは関数、クラス、ファイル等、呼び出して使用するオブジェクトです。実際に iter(callable, sentinel) が使われるのは、ファイルのオブジェクトの様ですので、この2つの引数のiter関数については、ファイルオブジェクトを紹介した後で再度説明します。

