集合型(set)とは
集合型のsetは、重複する要素を持たず順番もない集合を扱うデータ型で、波括弧{}またはset関数を使って定義します。
colors = {'red', 'blue', 'green', 'red', 'green',
'yellow', 'purple', 'red'}
colors, type(colors), len(colors)({‘blue’, ‘green’, ‘purple’, ‘red’, ‘yellow’}, set, 5)
上の例では ‘red’ や ‘green’ が定義文に複数入っていますが、出力された set型の変数 colors にはそれぞれ一つだけしか残っていません。この様に集合型は、重複する要素をもたない、順序づけられていない要素の集まりでコレクションと呼ばれる型の一つです。
type関数でデータ型を、len関数を使って要素数を確認することができます。
空の集合を生成するためには set() を使用する必要があります。{ } を使うと別章で述べる空の辞書型(dict)になります。
s, d = set(), {}
s, type(s), d, type(d)(set(), set, {}, dict)
集合型の作成に内包表記を使うこともできます。以下の例は colors に含まれる各要素(color)を更に文字(c)に分解して集合を作成する例です。
chars = {c for color in colors for c in color}
chars{‘b’, ‘d’, ‘e’, ‘g’, ‘l’, ‘n’, ‘o’, ‘p’, ‘r’, ‘u’, ‘w’, ‘y’}
set型の charsには一つ前で定義したcolorsに含まれている色(color)を構成している全ての文字(c)を、重複なしで格納しています。上記内包表記の式からも分かります通り、set型(colors)をfor文のinの後ろに使うことができます。for文の in の後には、シーケンス型以外にもコレクション型も使うことができます。
set型の出力は一応アルファベット順に並んでいますが、シーケンス(list, tuple, range, str)の様に先頭の要素をindexで抽出することはできません。set型のcharsにindexをつけてchars[0]とするとTypeErrorとなります。
set 型を list関数で list に変換することができます。
ls = list(chars)
ls, ls[0]([‘d’, ‘o’, ‘l’, ‘g’, ‘p’, ‘w’, ‘u’, ‘r’, ‘n’, ‘y’, ‘e’, ‘b’], ‘d’)
set関数でシーケンス型から重複を除いてset型(集合)を作成することができます。
print(set([3, 1, 2, 0, 2, 1]))
print(set('abracadabra')){0, 1, 2, 3}
{‘d’, ‘c’, ‘a’, ‘r’, ‘b’}
set型の真理値判定は、要素を持たない空集合のset()がFalse、それ以外の一つ以上の要素がある集合がTrueです。 {} はは次章で説明するdict(辞書)型の意味になりますので、set型の空集合はset()を使用します。
bool(set('ab')), bool(set()), type(set()), type({})(True, False, set, dict)
set型は要素の追加、削除が可能な mutable です。これに対して要素の変更ができないimmutableな集合型がfrozenset (frozen:凍りついた)で、以下の様にfrozenset関数を使って作成します。
fzs = frozenset('abracadabra')
fzs, type(fzs)(frozenset({‘a’, ‘b’, ‘c’, ‘d’, ‘r’}), frozenset)
以下に集合型の演算を示しますが、一部の要素の追加、削除に関する演算はfrozenset型では使うことができません。
set型の演算
set / frozenset 共通の演算
set型/frozenset型共通の演算を紹介します。これらも覚える必要はありませんが、一通り目を通してどの様なものがあるのかを掴んでおくのが良いかと思います。
参照元: https://docs.python.org/ja/3/library/stdtypes.html#set-types-set-frozenset
set / frozenset 共通の演算の実行例
実行例で用いた集合の関係は以下の図を参考にしてください。
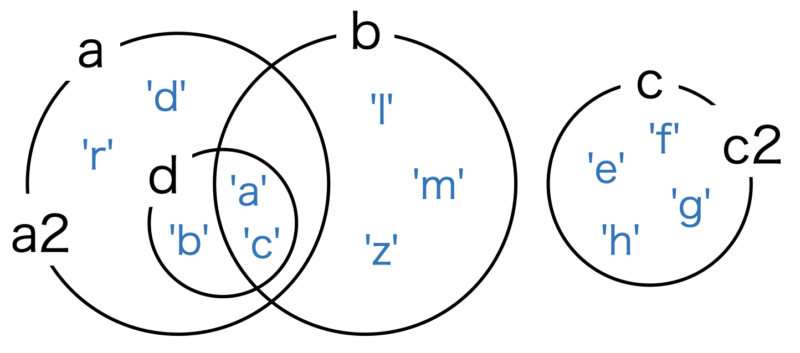
# len(s) : 集合 s の要素数( s の濃度)
a = set('abracadabra')
a, len(a)({‘a’, ‘b’, ‘c’, ‘d’, ‘r’}, 5)
# x in s : x が s 含まれるとき True
'c' in a, 'e' in a(True, False)
# x not in s : x が s 含まれるとき True
'c' not in a, 'e' not in a(False, True)
# set == other : set と otherが全く同じ要素を持つとき True
# set != other : set == other ではないとき True (一つでも異なる要素があるとき)
a2 = {'r', 'c', 'b', 'd', 'a'} # 順番を並べ替えても同じ
a == a2, a != a2(True, False)
b = set('alacazam')
print(b)
a == b, a != b{‘l’, ‘m’, ‘c’, ‘z’, ‘a’}
(False, True)
set と frozenset でも同じ要素を持つとき、例えば set(‘abc’) == frozenset(‘abc’) はTrueとなります。反対に、set(‘abc’) is frozenset(‘abc’) は型が違う、すなわち異なるオブジェクトとなり Falseとなります。
set('abc') == frozenset('abc'), set('abc') is frozenset('abc')(True, False)
以下の演算は、== と同様に set と frozenset の間でも集合同士の比較演算が可能です。
# .isdisjoint(other) : 集合が other と共通の要素を持たないとき True
c = {'e', 'f', 'g', 'h'}
a.isdisjoint(b), a.isdisjoint(c)(False, True)
# .issubset(other), set <= other
# : set の全ての要素が other に含まれるとき True
d = {'a', 'b', 'c'}
b.issubset(a), d.issubset(a), b <= a, d <= a(False, True, False, True)
ここで issubsetメソッドと演算子 <= は同じ演算として記載していますが、全く同じではありません。その違いは他の演算子も含め、まとめて後程説明します。
# set < other : set が other の真部分集合であるとき True
d < a, a2 < a(True, False)
# .issuperset(other), set >= other
# : other の全ての要素が set に含まれるとき True
a.issuperset(b), a.issubset(d), a >= b, a >= d(False, True, False, True)
# set > other : set が other の真上位集合であるとき True
a > d, a > a2(True, False)
次に、演算子として初めて | と & が出てきます。 | は「パイプ」と呼び「または」の意味で、& は「アンパサンド」と呼び「かつ」の意味です。
# .union(*others), set | other | ...
# : set と全ての other の要素からなる新しい集合(和集合)を返す
a.union(b, c), a | b | c({‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, ‘h’, ‘l’, ‘m’, ‘r’, ‘z’},
{‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, ‘h’, ‘l’, ‘m’, ‘r’, ‘z’})
上記 union の引数 *others の * の意味は複数の集合を渡すことができるという意味の表記です。
# .intersection(*others), set & other & ...
# : set と全ての other に共通する要素を持つ新しい集合(積集合)を返す
a.intersection(b, d), a & b & d({‘a’, ‘c’}, {‘a’, ‘c’})
# .difference(*others), set - other - ...
# : set に含まれて、かつ全ての other に含まれない要素を持つ新しい集合(差集合)を返す
a.difference(b, d), a - b - d({‘d’, ‘r’}, {‘d’, ‘r’})
# .symmetric_difference(other), set ^ other
# : set と other のいずれか一方だけに含まれる要素を持つ新しい集合(対称差集合)を返す
a.symmetric_difference(b), a ^ b({‘b’, ‘d’, ‘l’, ‘m’, ‘r’, ‘z’}, {‘b’, ‘d’, ‘l’, ‘m’, ‘r’, ‘z’})
# copy() : 集合の浅いコピーを返す
c2 = c
c3 = c.copy()
print('c:', c, id(c))
print('c2:', c2, id(c2))
print('c3:', c3, id(c3))c: {‘g’, ‘h’, ‘f’, ‘e’} 140446518262464
c2: {‘g’, ‘h’, ‘f’, ‘e’} 140446518262464
c3: {‘g’, ‘h’, ‘f’, ‘e’} 140446518353248
上記では、 c2 は単に = を使用したとき、c3 はcopyメソッドを使用した複製です。 id はオブジェクトの番号(番地)を表します。c と c2 は同じidで c3 は異なる id です。従って list の時と同様に、c2を変更すると、c も変更されてしまう現象がここでも発生します。後程確認します。
ブール演算子 or, and を使うと
set型の a, b から両方の要素からなる集合を作る場合には a.union(b) または a | b を使用します。ブール演算子を使って a or b とすると異なる出力になりますので注意が必要です。
a, b = set('abracadabra'), set('alacazam')
print('a.union(b): ', a.union(b),'\n',
'a | b: ', a | b,'\n',
'a or b: ', a or b, sep = '')a.union(b): {‘d’, ‘l’, ‘b’, ‘m’, ‘c’, ‘z’, ‘r’, ‘a’}
a | b: {‘d’, ‘l’, ‘b’, ‘m’, ‘c’, ‘z’, ‘r’, ‘a’}
a or b: {‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
a.union(b) と a | b は期待した通りの結果ですが、a or b は a がそのまま出力されます。
ブール演算子 or は練習問題_2_4で紹介した通り、オブジェクト自体をTrue(真)かFalse(偽)の判定をして、or の演算結果を被演算子 a, b のどちらかで出力する演算です。 a or b の場合は、a が真(True)のときは a, a が偽(False)のときは b を返します。この場合 a が真(True)なので a がそのまま出力されます。
同様に、set型の a, b から共通の要素からなる集合を作る場合には a.intersection(b) または a & b を使用します。ブール演算子の a and b は a が真(True)のときは b, a が偽(False)のときは a を返す演算ですので、出力は b となります。
a, b = set('abracadabra'), set('alacazam')
print('a.intersection(b): ', a.intersection(b),'\n',
'a & b: ', a & b,'\n',
'a and b: ', a and b, sep = '')a.intersection(b): {‘c’, ‘a’}
a & b: {‘c’, ‘a’}
a and b: {‘l’, ‘m’, ‘c’, ‘z’, ‘a’}
set 型のみの演算
こちらは集合の要素を追加・変更・削除に関する演算で、set型には適用できますが、frozenset型には適用できません。
参照元: https://docs.python.org/ja/3/library/stdtypes.html#set-types-set-frozenset
set 型のみの演算の実行例
実行例で用いた集合の関係は以下の図を参考にしてください。
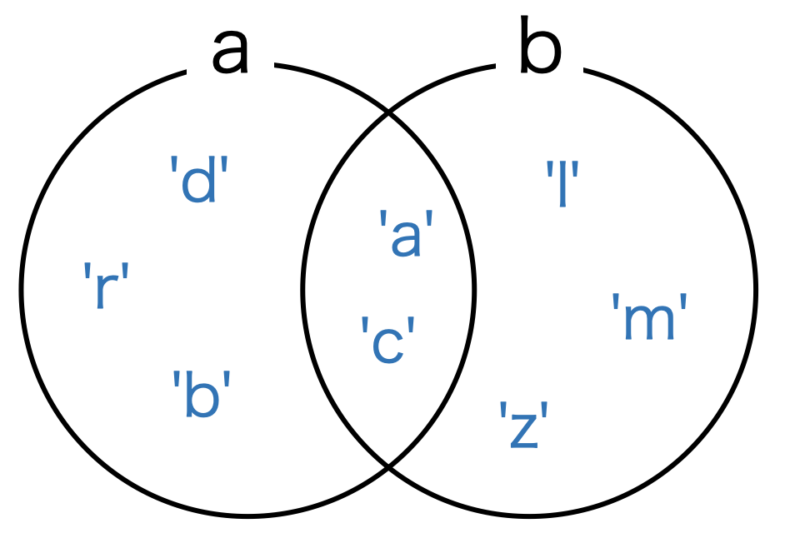
# .update(*others), set |= other | ...
# : 全ての other の要素を追加した和集合で set を更新
a, b = set('abracadabra'), set('alacazam')
print(a, 'id:', id(a))
a.update(b) # または a |= b
print(a, 'id:', id(a)){‘d’, ‘b’, ‘c’, ‘r’, ‘a’} id: 140446518433152
{‘d’, ‘l’, ‘b’, ‘m’, ‘c’, ‘z’, ‘r’, ‘a’} id: 140446518433152
updateメソッドまたは累算代入演算子の |= を上記の様に使用した場合、a 自体が b の要素が追加した和集合で更新されます。ここが前節のunionメソッドや代入演算子の | と異なる点です。unionや | を使う場合は、c = a.union(b) の様に改めて変数に代入しないと合成した集合は後で参照できませんが、update や |= は a そのものが変更されるので、改めて変数に代入する必要はありません。
また注意する点として、累算代入演算子の |= を使用して複数の集合を追加する場合は、
a |= b | c | d ..
の様に累算代入演算子の |= は最初だけ使用して2つ目からは | を使用します。 |= より | の方が演算の優先順位が高いので、 a |= (b | c | d .. ) と同じく b, c, d .. の和集合を先に計算してその結果と a の和集合を a に改めて代入していることになります。
copyについて
また、この演算の前後で a の id は変わりません。前節で触れたcopyメソッドが必要な訳をここで確認しましょう。
a, b = set('abracadabra'), set('alacazam')
a2 = a
a3 = a.copy()
print('a: ', a, ' id:', id(a), '\n',
'a2: ', a2, ' id:', id(a2), '\n',
'a3: ', a3, ' id:', id(a3), sep= '')
a |= b
print('\n','a: ', a, ' id:', id(a), '\n',
'a2: ', a2, ' id:', id(a2), '\n',
'a3: ', a3, ' id:', id(a3), sep= '')a: {‘d’, ‘b’, ‘c’, ‘r’, ‘a’} id:140446518433152
a2: {‘d’, ‘b’, ‘c’, ‘r’, ‘a’} id:140446518433152
a3: {‘c’, ‘d’, ‘r’, ‘b’, ‘a’} id:14044651843494
a: {‘d’, ‘l’, ‘b’, ‘m’, ‘c’, ‘z’, ‘r’, ‘a’} id:140446518433152
a2: {‘d’, ‘l’, ‘b’, ‘m’, ‘c’, ‘z’, ‘r’, ‘a’} id:140446518433152
a3: {‘c’, ‘d’, ‘r’, ‘b’, ‘a’} id:140446518434944
a2 は単に = を使用して a を代入したもの、a3 はcopyメソッドを使用した複製ですので、a と a2 の id は同じで a3 の id は異なります。ここで、a |= b として a に b の要素を追加します。すると同じidの a2 も a と同じくbの要素が追加されていますが、copyメソッドを使用した異なるidの a3 は a を変更しても影響は受けていないことが分かります。
set 型のみの演算の実行例(続き)
# .intersection_update(*others), set &= other & ...
# : 元の set と全ての other に共通する要素だけを残した積集合で set を更新
a, b = set('abracadabra'), set('alacazam')
print(a)
a.intersection_update(b) # または a &= b
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
{‘c’, ‘a’}
intersection_updateメソッドまたは累算代入演算子の &= を上記の様に使用した場合、a は a & b (a と b の共通要素)に置き換わります。累算代入演算子の &= を使用して複数の集合を適用する場合は、 a &= b & c & d .. となります。
# .difference_update(*others), set -= other | ...
# : other に含まれる要素を取り除いた差集合で set を更新
a, b = set('abracadabra'), set('alacazam')
print(a)
a.difference_update(b) # または a -= b
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
{‘d’, ‘b’, ‘r’}
累算代入演算子の -= を使用して複数の集合を適用する場合は、 a -= b | c | d .. となります。
# .symmetric_difference_update(other), set ^= other
# : どちらかにのみ含まれて、共通には持たない要素(対称差集合)で set を更新
a, b = set('abracadabra'), set('alacazam')
print(a)
a.symmetric_difference_update(b) # または a ^= b
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
{‘d’, ‘l’, ‘b’, ‘m’, ‘z’, ‘r’}
ここで注意すべき点は、対称差集合は2つの集合間の演算ですのでsymmetric_difference_updateメソッドの引数は一つ(otherのみ)です。
# add(elem) : 要素 elem を set に追加
a = set('abracadabra')
print(a)
a.add('z')
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
{‘d’, ‘b’, ‘c’, ‘z’, ‘r’, ‘a’}
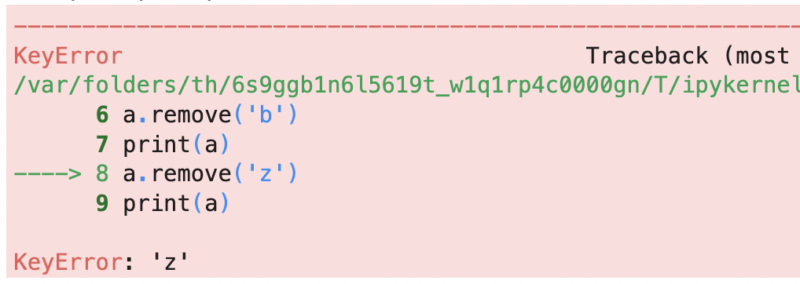
# remove(elem) : 要素 elem を set から取り除く
# elem が set に含まれていなとき KeyError
a = set('abracadabra')
print(a)
a.remove('b')
print(a)
a.remove('z')
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
{‘d’, ‘c’, ‘r’, ‘a’}
# discard(elem) : 要素 elem が set に含まれていれば、取り除く
a = set('abracadabra')
print(a)
a.discard('b')
print(a)
a.discard('z')
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
{‘d’, ‘c’, ‘r’, ‘a’}
{‘d’, ‘c’, ‘r’, ‘a’}
# pop() : s から任意の要素を取り除き、それを返す
# 集合が空のとき KeyError
a = set('abracadabra')
print(a, '\n')
while a:
print(a.pop(), a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
d {‘b’, ‘c’, ‘r’, ‘a’}
b {‘c’, ‘r’, ‘a’}
c {‘r’, ‘a’}
r {‘a’}
a set()
popメソッドは引数を取りませんので、常に .pop() という形で set型の後ろに置かれます。a.pop()とすると a から任意の要素を抜き取り a.pop()にはその抜き取った要素が入った状態となります。
while a: は a が空集合になって Falseと判定されるまで処理、この場合 print(a.pop(), a) を繰り返します。
# clear() : set の全ての要素を取り除く
a = set('abracadabra')
print(a)
a.clear()
print(a){‘d’, ‘b’, ‘c’, ‘r’, ‘a’}
set()
メソッドと演算子の違い
以下のset型の演算はメソッドと演算子の両方定義がされています。
| メソッド | 演算子 | 結果 |
|---|---|---|
| issubset(other) | set <= other | set の全ての要素が other に含まれるとき True |
| issuperset(other) | set >= other | other の全ての要素が set に含まれるとき True |
| union(*others) | set | other | … | 和集合を返す |
| intersection(*others) | set & other & … | 積集合を返す |
| difference(*others) | set – other – … | 差集合を返す |
| symmetric_difference(other) | set ^ other | 対称差集合を返す |
| update(*others) | set |= other | … | 和集合で更新する |
| intersection_update(*others) | set &= other & … | 積集合で更新する |
| difference_update(*others) | set -= other | … | 差集合で更新する |
| symmetric_difference _update(other) | set ^= other | 対称差集合で更新する |
これらのメソッドと演算子には一つ違いがあります。それはメソッドはイテラブルなオブジェクトを引数として使用することができますが、演算子でset型の演算を実行するには、被演算子は set型のオブジェクトである必要があります。
イテラブルなオブジェクトとは、要素を一度に 1 つずつ返せるオブジェクトです。これまで学んだオブジェクトのうち、シーケンス型(str, taple, range)や文字列(str)、そして今回の集合型(set)もイテラブルに含まれます。for文の in の後に使えるオブジェクトは全てイテラブルなオブジェクトとなります。
はじめに set と str の和集合を演算子 | で繋いでみます。
set('abracadabra') | 'alacazam'
同じ set と str に union を使ってみます。
set('abracadabra').union('alacazam'){‘a’, ‘b’, ‘c’, ‘d’, ‘l’, ‘m’, ‘r’, ‘z’}
今度はエラーとならずに ‘alacazam’ を set に変換して和集合を出力しています。
同じことを演算子の | を使うには set(‘abracadabra’) | set(‘alacazam’) とする必要があります。
和集合を例に説明しましたが、上表の和集合以外の演算についても同様ですので、時間がある方は確認してみてください。
練習問題_5_1 20個のボール
箱に20個のボールがあり、ボールには 1 から 20までの番号が書かれています。そこから目隠しでボールを一つ取り出して番号を入手する事象に関しする問題です。取り出す確率はどのボールも同じで、毎回取り出したボールは戻すことにします。
ここで、omg を標本空間(全ての番号の集合)、a2, a3, a5 は omg の中のそれぞれ 2, 3, 5の倍数の集合とします。また問題文は以下の様によく使われる集合の表記法で記載しています。
- a ∪ b:和集合、a ∩ b:積集合、a \ b:差集合、a △ b:対称差集合
- ac: a の補集合で、標本空間 \ a
- P(a): a の要素が取り出される確率
この時、以下の1番で omg, a2, a3, a5を出力し、2番以降は良く目にする集合に関する式に関して、左辺と右辺を出力させ、左辺 == 右辺 がTrueになることを確認してください。
- omg, a2, a3, a5 を出力
- a2 ∩ (a3 ∪ a5) == (a2 ∩ a3) ∪ (a2 ∩ a5)
- a2 ∪ (a3 ∩ a5) == (a2 ∪ a3) ∩ (a2 ∪ a5)
- (a2 ∪ a3)c == a2c ∩ a3c
- (a2 ∩ a3)c == a2c ∪ a3c
- a2 △ a3 == a2c △ a3c == (a2 ∪ a3) \ (a2 ∩ a3)
- P(a2 ∪ a3) == P(a2) + P(a3) – P(a2 ∩ a3)
確率の計算方法ですが、例えば a2が発生する確率P(a2) は
len(a2)/len(omg) (2の倍数のボールの個数)/(ボールの総数)
で計算します。
練習問題_5_2 条件付き確率
pythonでは和集合の演算子を | で表しますが、確率を表記する時に別な意味で | を使用しますので、その点を認識するためにこの問題を追加します。
AとBの2つの事象があり、P(B) > 0 のとき $$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$ をBを与えたときのAの条件確率(conditional Probability)と言います。ここで、紛らわしいのですがP(A|B)はBであるときのAの確率ということになります。
それでは、上記公式に従って以下の2つの確率を求めてください。
- P(a2|a3):1〜20の中の3の倍数のボールから2の倍数のボールを取り出す確率、変数名:p_a2_a3
- P(a3|a2):1〜20の中の2の倍数のボールから3の倍数のボールを取り出す確率、変数名:p_a3_a2

